Tutorials:3D Meshing Part I
| 3D Meshing Part I | |
|---|---|
| Author | WesHowe |
Contents |
Terms and Concepts
As a preface to the entire series, we will be illustrating basic concepts with MilkShape. While I am not "shilling" for the program: it works, it is cheap, and above all I know how to use it. There are many other 3D meshing programs available, some are free, some are very expensive and some are cheaper than MilkShape.
I am of the opinion that you get what you pay for. While free programs like Blender have a lot of features, ease-of-use is not one of the more outstanding qualities. On the high-end, programs like Maya and trueSpace have powerful features and are easy to use (not necessarily easy-to-learn), but their high cost places them in a category where only professionals and very determined hobbyists would consider purchasing them.
Orientation
3D computer graphics is a broad subject. Some parts are old and little used, other parts relate more to illustrations and art. We are going to focus on the parts that are used in the making of The Sims 2/3 game. Once someone understands all that, then moving further into other areas is much easier.We will start with the concept of space. When we mesh, we build our mesh in something we call object space. In simple terms, we have a spot on the ground underneath our object and we measure from there up, forward or to the side to the parts we will make. The "spot on the ground" is called the origin.
So we start at the origin, and we want to be able to determine any location above or below, in front or in back of, or on one side or another of our origin. We do this by creating an axis, actually three of them (axes), labeled by convention as X, Y and Z. This is our coordinate system.
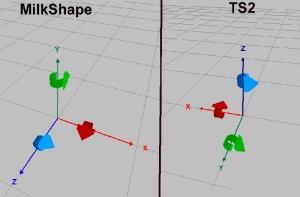
Which letter assigned to what direction is pretty important, and is the first point of confusion, because MilkShape and TS2 use different coordinate systems. The difference can be seen in the diagram to the right.
Scale
I printed that diagram out, and used loops of scotch tape to paste it on the computer desk just above my monitor. You might consider doing the same.
In the previous picture, the axes were colored and started at the origin, and the arrows point in the direction of increasing measure. To go in the opposite direction on any axis, we use negative values.
So, by using three numbers, we can describe where a place in our mesh is, in relation to our origin. By convention we will order the three numbers as X, Y and Z. So our origin is 0, 0, 0. And the location 1, 2, 3 would be 1 left of, 2 in front of and 3 above the game origin. The same coordinates in MilkShape would mean 1 right, 2 up and 3 in front of the origin. This is an important distinction, you need to know what coordinate system is in use.
And speaking of 1 left, 2 front and 3 above, what units? Feet, miles, inches, what? Actually it does and doesn't matter. The scale can be changed, so values only need to make sense in relation to the origin. But because we don't want to have to rescale something every time we want to export it and use it in our game, we will standardize on the scale the game uses, which is one unit equals one meter.
Not all objects in the game are scaled perfectly, since it is a game, not an architectural model. There is some latitude for the artists to tweak objects to make things look better, but if you design people or objects using that scale, they will fit in the game. The tiles themselves are one meter on a side.
Vertex
Now that we know which way is up, we can discuss the parts that make up a mesh. The first thing we will talk about is a point in 3D space. This point is like what you studied in geometry in the 9th grade or so, perhaps. It isn't meant to really be a thing, like a grain of sand or a speck of dust, it is just a place, infinitely small.
These point locations are used to define a vertex (plural vertices). The vertex is useless by itself, but we will use multiple ones to define the perimeter of a polygon.
These polygons are just like you studied in geometry also, a flat place of some number of sides. While high-end modelers allow the use of multiple forms of polygons, typically rectangles as well as triangles, in most games these are decomposed into triangles. Using multiple triangles you can define any polygon shape that can be drawn, using only the vertices (corner points) that are already defined. While defining a rectangle requires four vertices and a face definition of four, and decomposing this to triangles uses the same four vertices but requires six references, typically the database space required is not a lot bigger, because using multiple polygon types would require a value be stored with each that describes how many sides, reducing the six versus four to six versus five.
In 3D game rendering, speed is an even more important consideration than database (file) size, and the code to render just triangles is simpler and runs faster than more flexible modeling formats. Modelers such as Maya that can use quads or more all have options to allow the mesh to be decomposed into triangles (triangulate).
So in our meshing work here we will only talk about triangles, and in general will use the terms face, polygon and triangle interchangeably. They mean different things, but the way we are using them they are all mainly equivalent.
So a face in a mesh is one triangle, and each triangle needs three vertices. Note that I didn't say three unique vertices, those vertices can be shared with other triangles. And not even a unique set, because we can, and will, define the face as having two sides.
We will do this via the way we number things. Numbers are painful to some people, but we just need to understand how the values are laid out, and we can let the computer manage the math and tracking the locations out to six or more decimal places.
Face Index
So now we need to talk a little about the numbers. The locations, vertices, we defined earlier as being three values in XYZ order. I hinted above that they can go out to six or more decimal places. The programmers further define these as floats, or floating point numbers. For learning to mesh, we just need to know that they can look like 1 or 1.000357, each decimal part corresponding to a tenth (decimeter), hundredth (centimeter), thousandth (millimeter) and so on. Given the size of the computer screen three places is an invisible difference, but software uses finer values to ensure that errors to not accumulate during calculations that might add up to a discernible difference.
So now we defined the vertex as a set of three floats, and we defined a face as a set of three vertices, then we might just decide the simplest way to express this would be three sets of three, or nine values in a row, sort of XYZ(1), XYZ(2), XYZ(3). But to compact this, there is a scheme that greatly reduces the amount of memory required to store every face.
If we are building finite sized worlds, and we are because there are limits on how much data we can pack on our hard drives and more critically in computer memory, we can use some artificial limits that make the programming job more efficient and if the values are chosen properly we won't visibly impact our work. This is done in part by limiting the number of vertices to 65,536. In TS2/3, a mesh body might use 2,500 vertices, the hair and face another 2,500, or 5,000 or so, we can see that 65,536 is plenty big enough for low poly (low polygon count) games like TS2/3.
While there are some technical aspects of the game that allow this limit to be changed, I don't think any of the tools that exist outside of EA's shop are built to utilize them. UniMesh doesn't, because it is built on top of MilkShape, and MilkShape uses the same limits.
This is because we can pack up to 65,536 different values into just 16 bits, while the floating point numbers I talked of before take 32 bits (and a variety we do not use takes 64 bits). So by using fixed sets of values (short integers or shorts in programmerese) we can define each face using 3x16 bits and sharing locations instead of using 9x32 bits each.
For a single triangle the way we will lay things out, this takes more space, but starting with the second one on, we save space. Now, I have discussed this for a reason, because when we learn about welding and other aspects of meshing, we will leverage this knowledge.
So this is done by placing all the vertices in a single list, or 'pool. Like most computer stuff, we will start numbering this list with zero, instead of one. So each vertex still takes 3x32 bits. In the computer memory, this is managed as 12 consecutive bytes of memory for vertex 0 (the first) and then twelve more consecutive bytes for the second vertex (vertex 1) and so on for however many vertices are needed. We can then program the computer to count by twelves, so that 0 means the first twelve, 1 means the next twelve and so on.
So our faces only need to be saved using three small numbers each. While I don't want to make an illustration point-by-point, you can define the six faces needed for a pyramid (like the one on a dollar bill) with only five shared vertices. While the pyramid has only five sides, the bottom one is a square, and that has to be decomposed into two seperate triangle. Still there are only five points... one at the top, and four at the corners of the base. Every one of the points is used by three or more faces. And each face can be defined using only the three index values of the vertices.
Which brings up the concept of front and back sides. In order to simplify rendering, to speed the process, we can use a simple rule that allows the computer to quickly eliminate any triangles that aren't facing the screen (or camera). This process of eliminating stuff that should be on the other side from where we are looking from us called culling, and is accomplished by a clockwise rule. We do this by defining the order of the vertices we want to use such that when we look at it from the front the locations are in clockwise order, the back being counter-clockwise.
The computer can then sort the faces into just a list of faces that face more-or-less toward the camera, and since they are never drawn, making the ones that face the other way invisible (until we move or the object moves).
For our pyramid example above, as long as we never go inside the pyramid, all the parts we would ever be able to see at any one time will be rendered. From the inside, we would be able to see nothing. So if we have situations like that, we define another copy of each face, with the vertex order reversed. Some rendering problems require the vertex order to be reversed, and MilkShape has a built-in function to do this (we will discuss more later). Making things like hair require two-sided polygons, while bodies are generally left one-sided.
Comments and Clarifications
Question- Just to get this straight for all of us users; X which is left = 1, Y which is front = 2 and Z which is top = 3 in the sims2 ?? But in Milkshape the coordinates is turned? And to make it correct in game you would need to know that Y needs to go down so Z is in the up position while spinning X to the left twice? That way everything comes out as the way intended in the game? This way the intended object which has no real noticeable positioning can be position without worry that it is backwards? Correct?
Answer -'Well, if you build your "front" and "up" the way you want it to appear in MilkShape, the UniMesh exporter will do the conversions for you, automagically. If you export with the OBJ export format, you will have to tell SimPE to use XZY or everything is flipped.
The left/right inversion is ignored (perhaps unknown) by a lot of people, because for characters and many objects left and right are symmetrical.
The directions of rotation are for animation, and we will get there eventually, so having it on one chart helps. Again, the exporter knows to do these conversions, but when we discuss Y, we need to know which system (game or MS) we are talking about